Understanding mirrors puts you half ways towards fully understanding lenses as well. The same sort of rules apply, just with a few modifications.

Keep in mind that for an object to be considered a lens it must be made of a transparent material that has an index of refraction higher than air.

• That way it will be able to refract the light as it passes through.

The shape of a lens is named in a similar way to the naming of mirrors, it’s just a little more complicated.

• All lenses are broken into two broad groups, depending on whether they focus light at a point (converging lens), or spread it out (diverging lens).
• Converging lenses are always convex in shape, which means the centre is thicker than the edges.
• Diverging lenses are always concave in shape, which means the edges are thicker than the centre.

When drawing lenses in our sketches, you need to put in a principle axis, just like mirrors.

• You also need to add in a principle plane, a line that is perpendicular to the principle axis and runs length wise through the middle of the lens.
• We will be assuming that all refraction happens when the light reaches this principle plane.
• Although this is not true, it makes our sketches a lot easier to do, and it is pretty accurate for lenses that are fairly thin.
• I still draw in the focal point, but now I do it on both sides.

Figure 1: Double convex lens shown with principle axis, principle plane, and focal points.

Rule #1: Any ray through the focus will refract parallel to the principle axis.

Same basic idea as the rule you used for mirrors, but now the ray refracts and travels through the lens.

Figure 2

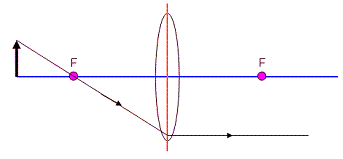
The light ray comes off of the object and goes through the focus. Notice that we did keep the ray moving in the same direction until it reached the principle plane in the lens. That’s where we bent the light so that it would travel parallel to the principle axis.

Rule #2: Any ray parallel to the principle axis will refract so that it passes through the focus.

Figure 3

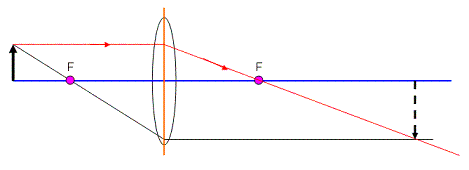
Just like for mirrors, we could stop now. We will look at how the third rule applies just to see what we get.

Rule #3: Any ray that passes through the centre of the lens will come out the other side without any refraction.

By centre, we mean where the principle axis and plane cross. The ray goes straight through as if nothing was there. This is because as much as the ray is refracted one way on one side of the lens, it will be refracted back the other way on the other side of the lens.

Figure 4

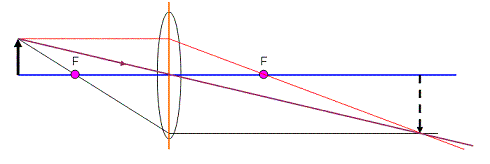
It looks like this ray agrees with our other two, so we must be doing ok!

Let’s look at an example using a diverging lens. We still use the same ideas, but we’ll have to look at where the image will be formed carefully.

Figure 5

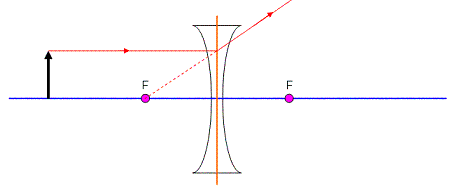
When I draw in the first ray parallel to the principle axis, it will hit the lens and diverge (be bent away). This must mean that if I extend the diverging ray back down as a dotted line, it will hit the focus on the object’s side.

Figure 6

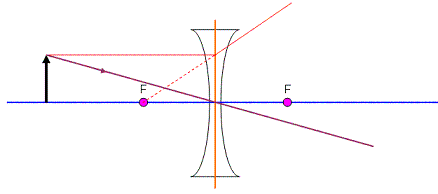
We can draw another ray that simply goes through the centre and see what happens…

Figure 7

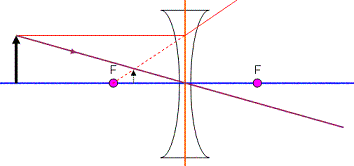
Notice where this line crosses the dotted line from the first ray? That’s where my image will appear. Since one of the rays is not truly there, the image will be virtual.

Figure 8

You can use the same formulas as you did for mirrors to do calculations with mirrors. Just keep the following rules in mind (they’re similar to the ones for mirrors…)

• d_o and d_i are positive for real objects and images, negative for virtual objects and images
• “f” is positive for convex (converging) lenses, and negative for concave (diverging) lenses.