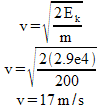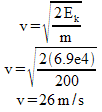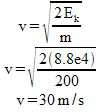A large number of questions you will do involve the Total Mechanical Energy of a system.
- Total mechanical energy is just the kinetic plus potential energy.
- As long as there are no outside forces unaccounted for, we know that the totals before and after will be equal.
Ek + Ep = Ek’ + Ep’
Note: the little ’ just means “after”.
We usually call this the Law of Conservation of Energy. It grows out of the Laws of Thermodynamics.
First Law of Thermodynamics
“Energy can not be created or destroyed,
only changed from one form to another.”
- This just basically means that if one thing loses energy, something else must be gaining energy. The opposite is also true.
- In an ideal situation this transfer of energy would be perfect and complete, but when was the last time you remember our universe being perfect…? This leads us to the second law …
Second Law of Thermodynamics
“In any energy conversion, there will always be some waste energy released as heat into the surrounding environment.”
In the second law we recognize that the total energy is constant, it’s just that some of the energy is released as unusable heat.
- This energy naturally flows from a hotter source to the cooler environment.
In most of the work we do, we assume that we are living in a “perfect” universe.
- This means that for the most part we will obey the first law, but ignore the second.
- There will be some situations when we give you enough information to use the second law, but we will be pretty specific about telling you.
- Most of the time we will say something about the friction involved, since this is the most common source for heat loss in your problems
Example 1: A person is sitting on a toboggan at the top of a 23.7m tall hill. If the person and toboggan have a total mass of 37.3 kg determine how fast they will be going when they reach the bottom of the hill. Assume there is no friction.
At the top of the hill the person isn’t moving, so Ek will be zero. At the bottom of the hill the Ep will be zero.
Ek + Ep = Ek’ + Ep’
½ mv2 + mgh = ½ mv’2 + mgh’
0 + (37.3kg) (9.81m/s2) (23.7m) = ½ (37.3kg) v’2 + 0
8.67e3 J = 18.7 v’2
v’ = 21.6 m/s
Notice how in this example all of the potential energy the object had at the top of the hill has been turned completely into kinetic energy at the bottom.
- It’s also possible to analyze how the potential energy steadily changes into kinetic energy during a fall…
Example 2: Wile E. Coyote is trying to drop a boulder off a cliff to hit the Roadrunner eating a bowl of birdseed. He wants to know the speed of the boulder at various points. He supplies you with the following blueprint…
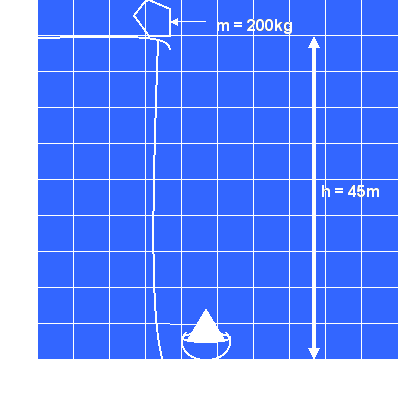
The Coyote wants you to determine the velocity of the boulder at several different heights above the ground, assuming no air resistance…
a) 45 m
b) 30 m
c) 10 m
d) 0 ma) Well, this one ain’t so tough! Since it’s sitting at the top of the cliff, its velocity is 0 m/s. It might be handy at this point to calculate how much Ep the boulder has.
Ep = mgh = 200kg (9.81m/s2) (45m) = 88290 J = 8.8e4 J
TOTAL ENERGY = 8.8e4 J
b) First, ask yourself how much Ep the boulder still has at 30m above the ground.
Ep = mgh = 200kg (9.81m/s2) (30m) = 58860 J = 5.9e4 J
That means that 8.8e4 J - 5.9e4 J = 2.9e4 J is missing, right?
Wrong! According to the conservation of energy, that energy must now be kinetic!
TOTAL ENERGY = 8.8e4 J
c) Again, calculate how much Ep you have at this new height of 10 m…
Ep = mgh = 200kg (9.81m/s2) (10m) = 19620 J = 2.0e4 J
That means that I have changed 6.9e4 J of energy into other forms… we’ll assume it all changed into kinetic energy.
TOTAL ENERGY = 8.8e4 J
d) By the time the boulder has reached the ground, all of its potential energy is gone (it’s zero metres above the ground!). We all know that when it actually hits the ground it will come to rest, but we are concerned with how fast it’s going when it is right at ground level but hasn’t actually touched the ground yet. We can assume that all of the potential energy the boulder had at the top is now kinetic energy at the bottom…
TOTAL ENERGY = 8.8e4 J
You could be finding the same answers based on kinematics formulas from Physics 20.
- In fact, you’ll find that conservation of energy gives you new ways to do many problems that you did with kinematics formulas…