Pendulums are a great example of periodic motion because they are simple to make and follow a pretty well established pattern of going back and forth the same way.

• It is true that if you hold a weight on the end of a string and let it swing like a pendulum it will eventually slow to a stop (because of friction).
• Still, by making pendulums with big masses, they can actually swing for a long time.

The periodic motion of something like a pendulum is also sometimes called Simple Harmonic Motion. "SHM" needs a force that causes an object to return to its equilibrium point. In the case of a pendulum this force is supplied by gravity.

• When the bob is pulled away from its equilibrium point, there is a component of the force due to gravity trying to move it back. As it gets closer to its equilibrium point this component of the force due to gravity decreases.

One of the first people to realize how physics could explain pendulums was Galileo.

• According to Galileo's own notes, he was visiting a local church one day when he happened to look at a person lighting the lamps that were hanging in the church.
• These lanterns were hanging from the roof by long chains. The lanterns themselves were quite heavy.
• The person lighting the lanterns was using a very long pole with a taper (fancy thin candle) on the end to light them… each time he reached up with the pole, he would nudge the lantern a bit which started it swinging.
• Galileo noticed that although all the lanterns were the same mass, the length of the chain they were dangling from seemed to change how fast they were swinging.
• In order to get some sort of measurement of the time it took them to swing, he actually used his own pulse to time them!

Although we have come a long way from the work that Galileo started, we still have a pretty simple equation that we can use to figure out how long it takes for a pendulum to swing…

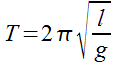
T = period of one swing (s)
ℓ = length of wire (m)
g = gravity (m/s²)

Notice that the mass of the bob (the weight at the end of a pendulum) is not in the formula.

• This agrees with Galileo’s observation that different masses on the end of the pendulum will not affect the period of the swing.
• The only thing a heavy bob does is keep the pendulum going for a longer period of time before stopping.
  • Think of it terms of inertia… a heavy bob has lots of inertia, so the pendulum swings back and forth for a long time before it stops. A lighter bob has little inertia, so it only swings for a little while before coming to rest at its equilibrium position.
• What really matters in the case of the pendulum is the length of the pendulum. If you’ve ever looked carefully at the pendulum on a Grandfather clock, you might have noticed that the bob can move up and down a little. This is to adjust the period of the pendulum so that the clock runs at the right speed.

Be careful when you are using this formula. Remember three things:

1. The period is the time it takes to complete one full swing… that means if you let go of the bob (the weight on the end), it will swing away from your hand and back to your hand. That’s one complete swing. Back to where it started and ready to move in the original direction again.
You can call the equilibrium point the equilibrium position or even rest position if you want.
2. This formula only works well if the pendulum is held at an angle of less than 15° from equilibrium position. As the angle gets further past 15° errors start to creep in.
3. Be careful if you need to solve it for “ℓ” or “g”. You’ll see in the following examples how to do this.

Example 1: What is the period of a pendulum that is 12.5 m long?

We will assume that it is on Earth…

T = 2 π √(l / g)
= 2 π √(12.5 / 9.81)
T = 7.09 s

Note: I used 3.14 for pi , which gave me three sig digs. Do not use the pi button on your calculator.

Example 2: We decide to measure gravity in a particular location on Earth. I use a 2.75m long pendulum and find that it has a period of 3.33 s. What is the acceleration due to gravity in this area.

T = 2 π √(l / g)
Do you get this same formula as this? Double check!

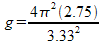
g = 9.78m/s²

Example 3: What length of pendulum would give me a period of one minute?

We can already make a pretty good guess that this is going to be a pretty long pendulum to take that long to swing.

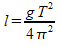
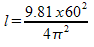
l = 895m

Yikes! Almost one kilometre long. And before you get grumpy about sig digs, notice that in the question I said “one minute”, which is by definition exactly 60 seconds, so I had an infinite number of sig digs there. Only the measurement of the acceleration due to gravity and pi have sig digs I need to worry about (3 on each).